人类的视觉系统是世界的一大奇迹，我们来看下面一组手写数字：

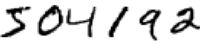
相信大部分人都可以毫不费力地认出这几个数字--504192。可别让这“毫不费力” 把你给骗了，在我们大脑的左右两个半脑中，有一片主视觉皮层V1，那里有 1亿4千万个神经元，中间有上百亿个连接。除了V1区域，人类视觉还用到了 整片整片的其他视觉皮层，V2、V3、V4、V5，它们一起进行着复杂的图像处理。 我们脖子上面，可是一台超级计算机，它在几亿年的进化过程中，已经很好地 适应了认知这个视觉世界的能力。识别手写数字其实并不容易，但由于人类的 视觉认知能力实在过于强大，大部分处理在潜意识就完成了，我们通常都意识 不到视觉系统所解决的问题有多么得复杂。

当你准备写一个计算机程序来识别上面这些数字时侯，视觉模式识别的难度就 凸显出来了。我们做起来这么容易的事情一下子变得无比困难：那些用于分辨 形状的简单直觉--比如9上面有一个圈，右边有一竖--这些通过算法来做都不 简单。并且当你试图精确描述这些规则的时候，你会发现总有这样那样的例外 或特殊情况，让人觉得这么做简直就是徒劳。

神经网络试图从不同的方向来解决这个问题，主要想法是利用大量已知的手写 数字，这些称为训练样本 (training examples)，

并籍此发展一个系统来学习这些样本。换句话讲，神经网络使用样本来自动 推算出识别这些数字的规则。而且，通过增加样本的数量，它可以学习更多 手写特征，并改善其识别率。上面只列出了100个样本，但通过几千，几百 万甚至上亿的样本我们可以打造一个更好的识别网络。

在这一章里，我们将编写一个计算机程序，实现一个可以识别手写数字的神经 网络。这个程序只有74行，而且没有使用任何特殊的神经网络库。不过这一 简短程序对手写数字的识别率可以高达96% 且无需任何人工干预。在后面的章节 我们将发展一些新的技术，让识别率增加到99%以上。事实上，最好的商用神经 网络工作得如此之好，它们已经被大量用在银行识别支票，邮局识别地址等场合了。

我们关注手写识别，因为这是学习神经网络一个很好的问题。而它又恰恰足够 有难度：不是一个简单的任务，但又没有难到需要特别复杂的方法。而且，它 非常适合拓展出一些更高级的技术，比如深度学习(deep learning)，因此本书 前后都会重复提到手写识别的问题。本书后面我们也将提到这些想法是如何应 用到其他方面的，比如计算机视觉，语音和自然语言处理等。

当然，如果这一章的目的仅仅是写一个计算机程序来识别手写数字，那我们也 不用这么多篇幅了。所以这里，我们将介绍一些神经网络的关键概念，比如 两种重要的神经元 (perceptron 和 sigmoid neuron)，以及被称作 Stochastic Gradient Descent（随机递解）的标准学习算法。这个过程中， 我将集中解释它们为什么是这么这样设计的，以便让你对神经网络有更直观的 感受。相比简单地列出其工作机制，我们需要用更多篇幅来讨论细节，但这些 细节将有助于加深了解。其中一点，在看完这一章后，我们将更好地理解什么 是深度学习 (Deep Learning)，以及为什么我们需要关注它。

感知神经元 (Perceptrons)

什么是神经网络？要回答这个问题，我们先介绍一种叫做感知神经元 (Perceptrons) 的人工神经元。感知神经元的概念由科学家 Frank Rosenblatt1 在50年 代和60年代提出，在之前 Warren McCulloch 和 Walter Pitts 的工作2 基础上发展而来3。我们今天更多使用其他类型的神经元，其中主要的一种 称为S型神经元 (Sigmoid Neuron)。我们很快将讲到S型神经元，在此之前， 了解一下 Perceptron 将有助于了解为什么S型神经元是这样定义的。

那么，感知神经元到底是怎么工作的呢？一个感知神经元可以接收多个二进制 输入: $x_1, x_2$, ...，并产生一个二进制输出

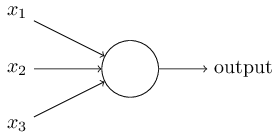
上面这个感知神经元有三个输入，$x_1, x_2, x_3$，但它通常可以有更多 或更少的输入。Rosenblatt 提出了一种计算输出的简单方法。他引入了权重 (weight) 的概念，$w_1, w_2$ ... 这些权重表示各个输入对输出所起的重要 程度。输出的结果为 0 还是 1，取决于权重和 $\sum_j w_j x_j$ 是否小于 或大于某个阈值。和权重一样，阈值也是神经元所特有的一个数字。更精确的 代数表达如下:

$$ \begin{eqnarray} \mbox{output} = \begin{cases} 0 \mbox{ if } \sum_j w_j x_j \leq \mbox{ threshold } \\ 1 \mbox{ if } \sum_j w_j x_j \gt \mbox{ threshold } \end{cases} \end{eqnarray} $$

这就是单个感知神经元的工作原理了。

以上是基本的数学模型。你可以认为感知神经元是一个根据输入权重做决定的 单元。举个不太现实但比较容易理解的例子，假设马上就要周末了，听说镇上 会有一个烧饼节，你很喜欢吃烧饼，并在考虑是不是要参加，你可能会根据下 面三个因素做出选择:

1. 天气好不好?
2. 你男朋友或者女朋友会不会陪你参加?
3. 举办地点离公交站近不近？(假设你没车)

我们用三个布尔变量 $x_1, x_2, x_3$ 来代表这些因素，比如 $x_1=1$ 表示 天气很好，$x_1=0$ 表示天气很糟。同样，$x_2=1$ 表示你的男女朋友会去， $x_2=0$ 表示不会去，$x_3$ 离公交站近或者远。

现在我们假设你太喜欢吃烧饼了，以至于你的男女朋友去不去，公交车站离得 远近你都无所谓。不过你对天气很挑剔，如果天气不好打死你也不会去。这种 情况我们依然可以用感知神经元来表示这一决定过程。一种方式是选择天气的 权重 $w_1=6$，并且另外两个因素的权重分别为 $w_2=2$ 以及 $w_3=2$。 $w_1$ 的值比较大意味着天气很重要，比你男女朋友是否同去或者离公交站远近 都来得更加重要。最后假定感知神经元的阈值为5。根据以上假设，这一神经元 就是你做决定的一个模型，天气好就输出1，天气不好输出0，你的男女朋友会不 会去、公交站近不近都不会对输出有任何影响。(译者：天气好 $x_1=1$ 意味着 $\sum_{j=0,1,2} x_j w_j \geq 6$ 总是大于阈值5)

通过改变权重和阈值，我们可以有不同的模型。比如，如果我们选择阈值3， 该神经元的输出除了考虑天气外，还会考虑你的男女朋友是否会去，以及公交站 远近的情况。换句话说，这是一个不同的决策模型，降低阈值表示你更愿意去。

显然，感知神经元并非一个完整的人类决策模型！但是这个例子展示了它是如何 根据不同条件的权重做出决策的。我们相信更复杂的神经元网络可以做出更精妙 的决策:

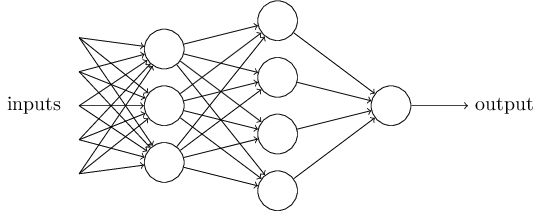
这个网络中第一列，我们称之为第一层神经元，将权衡输入产生三个简单的 输出。第二层中的每一个神经元将根据不同权重评估第一层的输出并产生进 一步的输出。于是，第二层的神经元可以比第一层作出更复杂更抽象的决定。 同理，第三层产生比第二层更复杂的输出。这样，多层的神经元网络可以帮助 做出相当复杂的决策。

在介绍感知神经元的时候，我们提到了单个神经元产生单个输出。但在上面 的网络中，它们看上去有多个输出，这只是方便表示某个神经元的输出被连接 到其他多个神经元的输入而已，事实上这些神经元的确只有一个输出。 画成单条输出线然后再分叉不太美观。

现在我们再来简化一下感知神经元的描述。写成 $\sum_j w_j x_j > \mbox{ threshold}$ 貌似有些复杂，我们可以有两种简化。第一，我们写成点积 (dot product) 的形式，$ w \cdot x \equiv \sum_j w_j x_j$，其中 $w$ 和 $x$ 分别是 权重和输入的向量形式。第二，把阈值搬到不等式左边，并把它叫做神经元 的偏差(bias)，$ b \equiv -threshold $。这样我们可以重写公式:

$$ \begin{eqnarray} \mbox{output} = \begin{cases} 0 \mbox{ if } w \cdot x + b \leq 0 \\ 1 \mbox{ if } w \cdot x + b \gt 0 \end{cases} \end{eqnarray} $$

你可以把偏差(bias)理解为是否容易输出1。生物学上来说，就是 让神经元激活(fire)的难易程度。对于一个偏差很大的神经元，让它产生1 会相当容易。但如果偏差是一个很大的负数，产生1就会相当困难。显然， 引入偏差仅仅是对神经元的描述作了一点小小的改变，后面我们将看到 它可以帮助进一步简化。因此从这里开始我们都将只用偏差(bias)而不 再用阈值了。